В медицинской литературе широко используются понятия медиана и интерквартильный размах, а в представлении данных – ящичковые диаграммы. Ниже мы приводим разъяснения по этому поводу.

В медицинских публикациях при описании данных чаще всего можно встретить представление числовых значений (например, артериального давления, уровня гемоглобина, возраста и т.д.) в виде среднего и стандартного отклонения, что отражается как М±σ (например, 136±12). В такой записи «М» означает среднее, а σ – стандартное отклонение. Это описание данных возможно только для признаков, распределение которых носит нормальный характер (рис 1а) – чаще всего это касается роста, веса, возраста и проч.

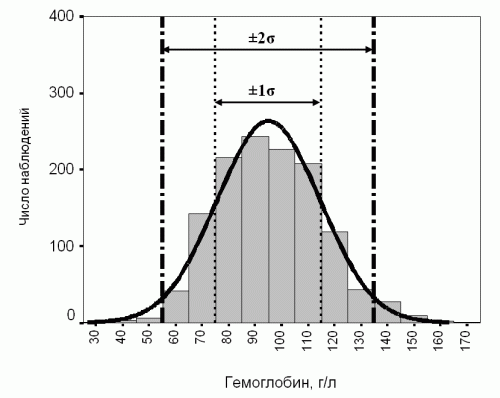
Рис. 1а. Пример нормального распределения (среднее 95,0, стандартное отклонение 20,0 г/л). Серыми столбцами показано распределение уровня гемоглобина. Колоколообразная кривая над столбцами соответствует кривой нормального распределения.

При нормальном распределении все значения признака можно расположить в форме симметричной колоколообразной кривой (рис. 1а). При этом в пределах одного стандартного отклонения от среднего находится 68% всех значений признака (для примера на рисунке 1а в интервале 75-115 находится 68% всех значений), в пределах двух стандартных отклонений от среднего находится 95% всех значений признака (для примера на рисунке 1а это интервал 55-135 г/л), и в пределах трех стандартных отклонений находится 99,5% всех значений признака.

Однако в медицине встречаются и данные, распределение которых отлично от нормального. В качестве характерного примера можно привести длительность наблюдения пациентов. На начальных сроках наблюдения пациентов всегда больше, а затем их количество уменьшается вследствие потери из наблюдения, смерти, и других причин. Такое распределение показано на рис 2а. Можно видеть, что кривая нормального распределения абсолютно не соответствует реальной картине, отраженной серыми столбцами.

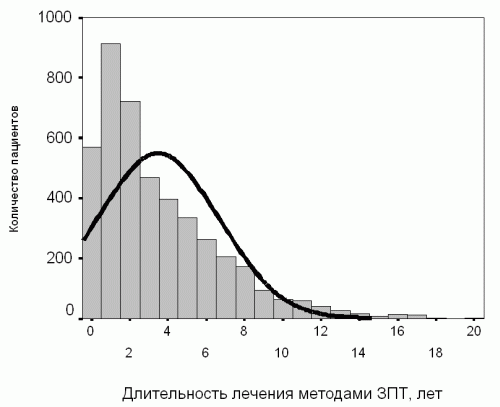
Рис. 2а. Пример распределения, отличного от нормального: длительность наблюдения 4389 пациентов.

Для таких распределений понятия среднее и стандартное отклонение утрачивают смысл, поскольку они дают неправильное описание распредения переменной. Так, для примера на рисунке 2а среднее составляет 3,5 г., а стандартное отклонение 3,2 года. Получается, что 95% пациентов должны иметь срок наблюдения от «минус» 2,9 г. до 9,9 г. Вполне ясно, что отрицательных сроков наблюдения не бывает. Даже в интервал одного стандартного отклонения, в котором должно находится 68% всех значений, явно попадает около 80% всех наблюдений. Отличительной чертой распределения, отличного от нормального, является несимметричное по отношению к среднему значению распределение признака («скошенность») либо наличие явно выбивающихся из общей картины значений.

Распределения, отличные от нормального, принято описывать при помощи медианы и интерквартильного размаха. Медиана – это значение признака, которое делит весь ряд значений пополам, то есть половина значений признака меньше медианы, и половина  – больше ее. Интерквартильный размах – это интервал между 25 и 75 процентилями, то есть четверть всех значений признака будут меньше 25 процентили, а четверть – больше 75 процентили. Таким образом, интерквартильный размах содержит «центральные» 50% значений признака.

Для длительности наблюдения, показанного на рисунке 2а, медиана составляет 2,5 года и интерквартильный размах 1,0 – 5,1 лет. Это означает, что половина всех больных находилась на лечении гемодиализом 2,5 года. Четверть всех больных – менее одного года, и четверть всех больных – более 5,1 года. Это описание правильно характеризует реальное распределение признака.

В принципе, понятие медианы и интерквартильного размаха вполне применимо и к нормальному распределению. В этом случае медиана будет равна среднему, а в пределах интерквартильного размаха будет находиться чуть меньше значений (50% всех значений), чем в пределах одного стандартного отклонения (68% всех значений).

Для распределений, отличных от нормального, не подходит и графическое отображение данных, принятое для нормального распределения. Среди нескольких вариантов, подходящих для визуального представления данных любого распределения, на наш взгляд, наиболее удобны ящичковые диаграммы.

На рисунке 3а показана ящичковая диаграмма. Ящичек закрашен серым цветом. Его нижняя граница является 25 процентилью, верхняя – 75 процентилью. Горизонтальная черная черта, пересекающая ящичек – это медиана. Как видим, медиана делит ящичек на две неравные части – значит в распределение, отображенное на рисунке 3а, носит неправильный характер. От ящичка отходят «усы». В примере на рисунке 3а нижний «ус» отражает интервал, в котором находятся 25% самых низких значений – от 9 до 17. Следует обратить внимание, что над верхним «усом» имеются две точки – выбросы (так обозначаются значения признака, сильно выделяющиеся из его общей совокупности). Поэтому верхний «ус» отражает интервал, в котором находятся 22,2% (25% минус два значения, которые составляют 2,8%). Таким образом, если выбросов нет, то «ус» отражает интервал, в котором находятся 25% всех наблюдений. Если же выбросы имеются, то «ус» отражает интервал, в котором находятся значения от квартили до величины, которая меньше, чем полторы длины ящичка (в примере на рис. 3а это интервал 27-42 года). На рисунке 3а также видно, что «усы» имеют разную длину. Это также говорит о том, что распределение возраста к началу гемодиализа для данной патологии носит ненормальный характер.

Следует отметить, что значения среднего и стандандартного отклонения чувствительны к выбросам, и могут значительно меняться при наличии экстремальных значений в ряду данных. Описание данных при помощи медианы и интерквартильного размаха позволяет избежать влияния выбросов.

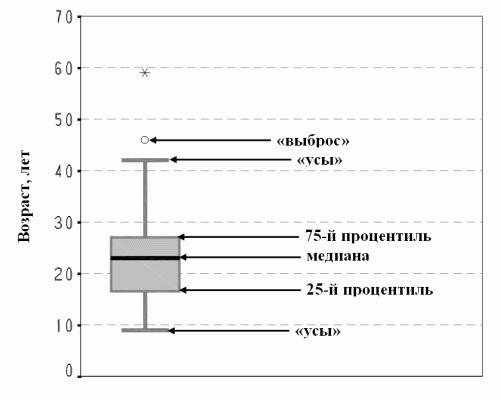
Рис. 3а. Распределение возраста больных с врожденной и наследственной патологией почек, впервые начавших лечение гемодиализом в 2001 г.

В качестве еще одной демонстрации преимущества ящичковой диаграммы, медианы и интерквартильного размаха при представлении данных рассмотрим распределение диастолического артериального давления у больных, находившихся на гемодиализе к декабрю 2001 года (рисунок 4а).

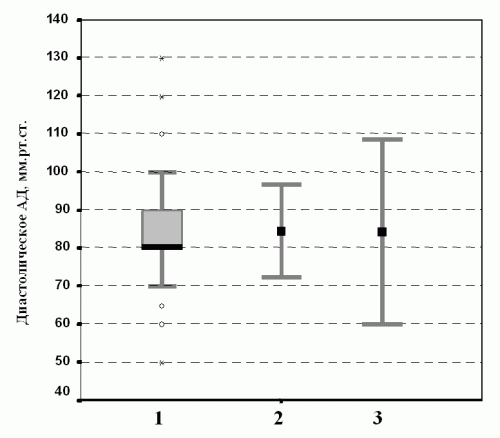
Рис. 4а. Распределение значений диастолического артериального давления у больных на гемодиализе к декабрю 2001 года (1274 наблюдения). Цифры под рисунком обозначают: 1 – ящичковая диаграмма, 2 – среднее±стандартное отклонение, 3 – среднее ± два стандартных отклонения.

Ящичковая диаграмма на рисунке 4а имеет одинаковые «усы», однако медиана совпадает с 25-й процентилью, и в области как минимальных, так и максимальных значений имеются выбросы. Это говорит о том, что распределение носит ненормальный характер. Факт совпадения медианы и 25-й процентили объясняется довольно просто. Диастолическое давление ниже 75 мм. рт. ст. имеют 19,1% пациентов, а давление 80 мм.рт.ст. – 35,2% больных. Таким образом, и медиана и 25-ая процентриль равны 80 мм.рт.ст.

На рисунке 4а показаны также графики, используемые для представления данных нормального распределения. Один из них демонстрирует среднее значение АД для той же группы больных и стандартное отклонение от среднего (обозначено цифрой 2), а другой – среднее и два стандартных отклонения (под цифрой 3). Среднее составляет 84 мм. рт. ст, стандартное отклонение – 12 мм.рт.ст. Хотя среднее отличается от медианы всего на 4 мм.рт.ст., для популяционных исследований это является весьма существенной разницей, которая может приводить к неправильной интерпретации результатов. Кроме того, хотя границы стандартных отклонений и близки к реально имеющимся данным, они никак не отражают имеющуюся неоднородность распределения значений артериального давления.

Учитывая, что ящичковые диаграммы хорошо отражают как нормальное, так и ненормальное распределения, выявляют крайние значения признака и более информативны в представлении частоты встречаемости отдельных значений, они широко используются при отображении числовых признаков.

---

* Приводится с изменениями, впервые опубликовано как приложение к отчету о состоянии ЗПТ (Бикбов Б.Т., Томилина Н.А. О состоянии заместительной терапии больных с хронической почечной недостаточностью в Российской Федерации в 2001 г. Нефрология и диализ 2004; 6: 4-42)

Обсудить | Рекомендовать другим | Похожие статьи | Распечатать .

Рекомендовать в

Aug 9th, 2010

Метки: графики, медицинская статистика, описательная статистика